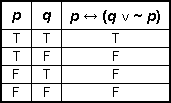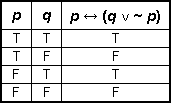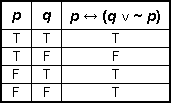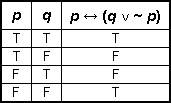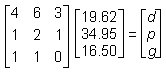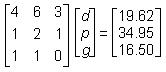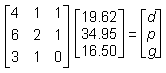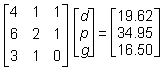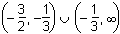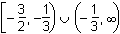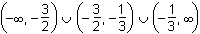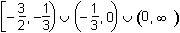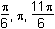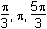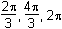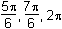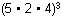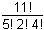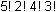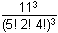Study Guide

Field 027: Mathematics
Sample Multiple-Choice Questions

Expand All | Collapse All

The following reference material will be available to you during the assessment:

Competency 0001
Understand mathematical problem solving.

In four half-cup samples of a cereal containing dried cranberries, the numbers of cranberries were 17, 22, 22, and 18. Nutrition information on a box of this cereal defines the serving size as 1 cup or 53 grams. If a box contains 405 grams, which of the following is the best estimate of the number of cranberries in one box of this cereal?

  1. less than 300
  2. between 300 and 325
  3. between 326 and 350
  4. more than 350
Answer
Correct Response: B.
This question requires the examinee to analyze the use of estimation in a variety of situations (e.g., rounding, area, plausibility). There are approximately 20 cranberries per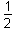 cup, or 40 cranberries per cup. The number of cups in a box is 405 ÷ 53, which is approximately equal to 400 ÷ 50 = 8 (rounding both the numerator and denominator down minimizes the error). Thus the approximate number of cranberries in a box of this cereal is 8 × 40 = 320, which is within the interval of response B.
Competency 0002
Understand mathematical communication, connections, and reasoning.

Given statements p and q, which of the following is the truth table for the compound statement p ↔ (q ∨ ~p)?





Answer
Correct Response: A.
This question requires the examinee to apply principles of logic to solve problems. First a truth value column for ~p is computed as F, F, T, T (in vertical order). Then this column is used to compute truth values for the statement q ∨ ~p: T, F, T, T. Finally, this result is used to compute truth values for the full expression p ↔ (q ∨ ~p): T, F, F, F.
Competency 0003
Understand number theory.

If p and q are prime numbers and 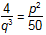what is the value of (p + q)?

  1. 5
  2. 7
  3. 8
  4. 9
Answer
Correct Response: B.
This question requires the examinee to apply the principles of basic number theory (e.g., prime factorization, greatest common factor, least common multiple). The variables can be isolated by multiplying both sides of the equation by 50q3, which yields 200 = p2q3. If p and q are both prime, then p2q3 is the prime factorization of 200. Since 200 = 25 × 8 = 52 × 23, and 5 and 2 are both primes, p must be 5 and q must be 2, so p + q = 5 + 2 = 7.
Competency 0004
Understand relations and functions.

Which of the following equations represents the inverse of y = ?

  1. y =
  2. y =
  3. y =
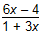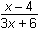
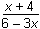
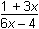
  4. y =
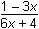
Answer
Correct Response: B.
This question requires the examinee to perform operations with functions, including compositions and inverses. To find the inverse of a function of the form y = f(x), the original equation is rearranged by solving it for x as a function of y: y =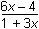 ⇒ y(1 + 3x) = 6x – 4 ⇒ y + 3xy = 6x – 4 ⇒ y + 4 = 6x – 3xy ⇒ y + 4 = x(6 – 3y) ⇒ x = 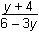. Exchanging the variables x and y results in the inverse function f–1, y =
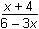
Competency 0005
Understand linear, quadratic, and higher-order polynomial functions.
  Order 1 Order 2 Order 3
soft drink 4 6 3
large pizza 1 2 1
garlic bread 1 1 0
Total Cost $19.62 $34.95 $16.50

Given the table of orders and total costs above, and that there is a solution to the problem, which of the following matrix equations could be used to find d, p, and g, the individual prices for a soft drink, a large pizza, and garlic bread respectively?





Answer
Correct Response: D.
This question requires the examinee to solve systems of linear equations or inequalities using a variety of methods. The system of linear equations can be solved using matrices. Each order can be expressed as an equation, with all three equations written with the variables in the same sequence. The first order is represented by the equation 4d + p + g = 19.62, the second order by 6d + 2p + g = 34.95, and the third order by 3d + p = 16.50. The rows of the left-hand matrix contain the coefficients of d, p, and g for each equation: (4 1 1), (6 2 1), and (3 1 0). The middle matrix contains the variables, d, p, g. The right-hand matrix vertically arranges the constants of the equations.
Competency 0006
Understand exponential and logarithmic functions.

Which of the following is equivalent to the equation 3 log10 x – 2 log10 y = 17?

  1. 3x – 2y = 1017
  2. x3 – y2 = 1017
  3. = 1017
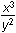  4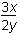. = 1017
Answer
Correct Response: C.
This question requires the examinee to apply the laws of exponents and logarithms.
Nloga M = loga MN ⇒ 3log10 x = log10 x3 and 2log10 y = log10 y2.
Loga M – loga N ⇒ loga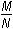 ⇒ log10 x3 – log10 y2 = log10 .
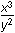Since loga M = N is equivalent to aN = M, then log10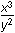 = 17 is equivalent to 1017 = .
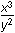Competency 0007
Understand rational, radical, absolute value, and piece-wise defined functions.

Which of the following represents the domain of the function f(x) = ?

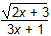Answer
Correct Response: B.
This question requires the examinee to analyze rational, radical, absolute value, and piece-wise defined functions in terms of domain, range, and asymptotes. Unless otherwise specified, the domain of a function is the range of values for which the function has a real number value. A rational function must have a nonzero denominator, and solving the equation 3x + 1 = 0 yields 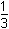x = –. Thus this value must be excluded from the domain. The radical expression in the numerator must have a non-negative argument and solving the inequality 2x + 3 ≥ 0 yields x ≥ –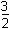. Putting these two results together results in – 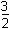≤ x < – 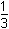or x > –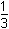. The "or" represents the union of the two sets defined by the inequalities, or the union of the two intervals.
Competency 0008
Understand measurement principles and procedures.

The shape of the letter B is designed as shown below, consisting of rectangles and semicircles.



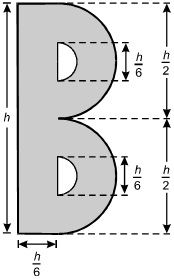
Which of the following formulas gives the area A of the shaded region as a function of its height h?

  1. A = h2
  2. A = h2
  3. A = h2
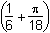
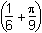
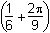
  4. A = h2
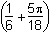
Answer
Correct Response: A.
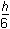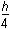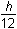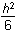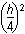This question requires the examinee to apply the concepts of perimeter, circumference, area, surface area, and volume to solve real-world problems. The total area of the letter B can be viewed as the area of an h × rectangle plus the area of a circle with radius minus the area of a circle with radius , or + π – π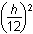. This simplifies to 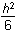+ 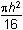– 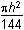and further to h2 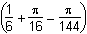and h2 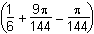and h2.
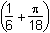Competency 0009
Understand Euclidean geometry in two and three dimensions.

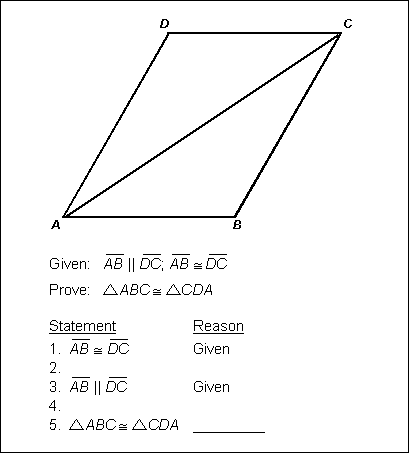
There is a diagram of a geometric proof.
The figure is a parallelogram, A B C D. The angles at A and C are acute, and a diagonal is drawn from A to C. The proof reads as follows.
Given: Line segment A B is parallel to line segment D C, line segment A B is congruent to line segment D C.
Prove: Triangle A B C is congruent to triangle C D A.
Statement 1. Line segment A B is congruent to line segment D C. Reason, Given.
Statement 2. Blank. Reason, blank.
Statement 3. Line segment A B is parallel to line segment D C. Reason, Given.
Statement 4. Blank. Reason, blank.
Statement 5. Triangle A B C is congruent to triangle C D A. Reason, blank.

In the proof above, steps 2 and 4 are missing. Which of the following reasons justifies step 5?

  1. AAS
  2. ASA
  3. SAS
  4. SSS
Answer
Correct Response: C.
This question requires the examinee to analyze formal and informal geometric proofs, including the use of similarity and congruence. The side-angle-side (SAS) theorem can be used to show that ΔABC and ΔCDA are congruent if each has two sides and an included angle that are congruent with two sides and an included angle of the other. In the diagram AB and DC are given as congruent, and the missing statement 2 is that AC is congruent to itself by the reflexive property of equality. The included angles ∠BAC and ∠DCA are congruent because they are alternate interior angles constructed by the transversal AC that crosses the parallel line segments AB and DC. Thus ΔABC and ΔCDA meet the requirements for using SAS to prove congruence.

Competency 0010
Understand coordinate and transformational geometry.

The vertices of triangle ABC are A(–5, 3), B(2, 2), and C(–1, –5). Which of the following is the length of the median from vertex B to side AC?

  1. 4
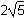
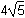
Answer
Correct Response: C.
This question requires the examinee to apply concepts of distance, midpoint, and slope to classify figures and solve problems in the coordinate plane. The midpoint of side AC where its median intersects is computed as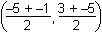 = (–3, –1). The distance from B(2, 2) to (–3, –1) is computed as d = .

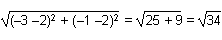Competency 0011
Understand trigonometric functions.

Which of the following are the solutions to 2 sin2 θ = cos θ + 1 for 0 < θ ≤ 2π?

Answer
Correct Response: B.
This question requires the examinee to manipulate trigonometric expressions and equations using techniques such as trigonometric identities. Since sin2 θ = 1 – cos2 θ, 2 sin2 θ = cos θ + 1 ⇒ 2(1 – cos2 θ) = cos θ + 1 ⇒ 2 cos2 θ + cos θ –1 = 0 ⇒ (2 cos θ – 1)(cos θ + 1) = 0 ⇒ cos θ =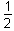 or cos θ = –1. Thus for 0 < θ ≤ 2π, θ = 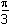, , 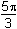or π.
Competency 0012
Understand differential calculus.

If f(x) = 3x4 – 8x2 + 6, what is the value of ?

  1. –4
  2. –1
  3. 1
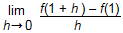  4. 4
Answer
Correct Response: A.
This question requires the examinee to analyze the derivative as the slope of a tangent line and as the limit of the difference quotient. The limit expression is equivalent to the derivative f'(1). Since it is much easier to evaluate the derivative of a polynomial, this is preferred over evaluating the limit expression. f'(x)= 12x3 – 16x, so f'(1) = 12 – 16 = –4.
Competency 0013
Understand integral calculus.

A sum of $2000 is invested in a savings account. The amount of money in the account in dollars after t years is given by the equation A = 2000e0.05t. What is the approximate average value of the account over the first two years?

  1. $2103
  2. $2105
  3. $2206
  4. $2210
Answer
Correct Response: A.
This question requires the examinee to apply integration to solve real-world problems. The average value of a continuous function f(x) over an interval [a, b] is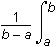 f(x)dx. Since the independent variable t represents the number of years, the average daily balance over 2 years will be 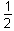of the integral of the function evaluated from 0 to 2:
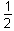
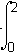2000e0.05tdt = 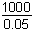(e0.1 – 1) ≈ 2103.
Competency 0014
Understand principles and techniques of statistics.

Which of the following statements describes the set of data represented by the histogram below?

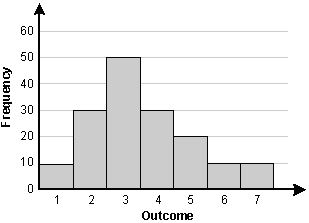
  1. The mode is equal to the mean.
  2. The mean is greater than the median.
  3. The median is greater than the range.
  4. The range is equal to the mode.
Answer
Correct Response: B.
This question requires the examinee to analyze data in a variety of representations. The mean can be calculated as [10(1) + 30(2) + 50(3) + 30(4) + 20(5) + 10(6) + 10(7)] ÷ 160 = 3.5625. The median is the 50th percentile, which is 3. The mode is the most frequent value, which is 3. The range is 7 – 1 = 6. Thus "the mean is greater than the median" is the correct response.
Competency 0015
Understand principles and techniques of probability.

The heights of adults in a large group are approximately normally distributed with a mean of 65 inches. If 20% of the adult heights are less than 62.5 inches, what is the probability that a randomly chosen adult from this group will be between 62.5 inches and 67.5 inches tall?

  1. 0.3
  2. 0.4
  3. 0.5
  4. 0.6
Answer
Correct Response: D.
This question requires the examinee to analyze uniform, binomial, and normal probability distributions. A normal distribution is symmetric about the mean. Thus if 20% of the heights are less than 62.5 inches (2.5 inches from the mean), then 20% of the heights will be greater than 67.5 inches (also 2.5 inches from the mean). Thus 100% – (20% + 20%) = 60% and the probability is 0.6 that the adult will be between 62.5 and 67.5 inches tall.
Competency 0016
Understand principles of discrete mathematics.

Five different algebra textbooks, two different calculus textbooks, and four different geometry textbooks are to be arranged on a shelf. How many different arrangements are possible if the books of each subject must be kept together?

Answer
Correct Response: C.
This question requires the examinee to apply concepts of permutations and combinations to solve problems. If the books in each of the 3 subjects must be kept together, then the number of ways the groups of books can be arranged by subject is represented by 3!. If there are n books within a subject, the number of ways the books can be arranged is n!. Thus the algebra books can be arranged in 5! different ways, the calculus books can be arranged in 2! different ways, and the geometry books can be arranged in 4! different ways. Since there is independence between the different arrangements computed, the total number of ways the books can be arranged is the product of all the factorials 3! 5! 2! 4! which is equivalent to 5! 2! 4! 3!.